1. Introduction
he medical image registration process is used to estimate the deformation between the images while considering the domain specific Information into consideration. A closer look at the problem statement intuitively reveals two methods of solving it. The first method operates directly on two different images have intensity values called intensity based registration [1], continuously transforming the entire image to align it with the other. When desirable alignment is obtained for the respective transformation, the optical representation is considered to be registered. These methods are called area based methods [2,3]. The second method relies on a few salient points which are most prominent in both the images. The goal here is to estimate the deformation based on the corresponding pairs of points/regions across the images.
These are known as feature-based medical picture based on brain methods, have gained popularity over the area based methods These methods [4] are more robust to illumination changes, a partial overlap between the images, occlusion, alterations in background, and viewpoint. Area-based methods are still preferred over feature based techniques, despite these advantages in the medical domain due to two main factors: 1) Its ability to handle local deformations, especially with the case of human organs. 2) Its capability of Dealing with information from different imaging sources.
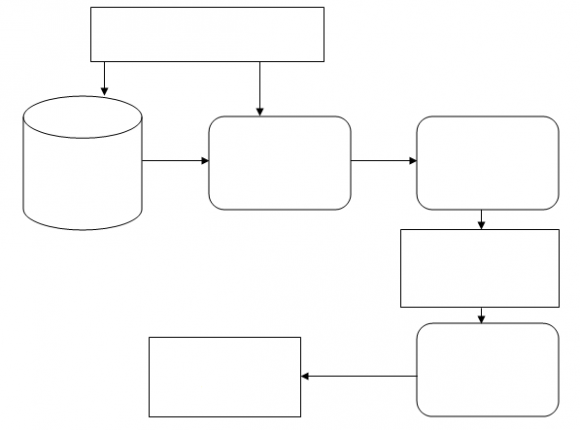
2. Fig. 1: Image Registration Process a) Transformation
Transformation step is to determine the position of corresponding points in reference and sensed images, Medical Image Registration (MIR) is considered as a combination of translation, rotation, and scaling parameters. Image registration methods employ transformations such as rigid, affine and elastic (nonrigid transformations [5]. The rigid transformation considers t x and t y translations along the x-axis and yaxis, and a rotational angle ? for the registration process [6]. It assumes that the subject in the image maintains its shape and size [7]. Affine transformations offer a high degree of flexibility in accommodating linear distortions by allowing and shearing in addition to translation and rotation [8]. The non-rigid transformation provides more degree of freedom as compared to rigid and affine transformation.
3. b) Optimization
Optimization problem is formulated by a number of parameters used for transformation [9] to get the maximum value of similarity, for a given registration process. The choice of the transformation is dependent on the type of application and its geometrical complexity (i.e., degrees of freedom). Although an exhaustive search guarantees an optimal solution, its computational expense is proportional to the size of the search space as well as the number of parameters used for transformation and, hence, becomes infeasible as they increase [10]. Therefore, these forms the motivation to explore refined search strategies or optimization methods which can help to find the maximum value for a given similarity measure.
Optimization method should be reliable and be capable of finding the best possible transformation quickly [11]. Many optimization methods have been introduced and adopted for the registration process, by the transformation parameters, similarity measure, time restrictions and required accuracy of registration.
4. c) Similarity Measure
Similarity measure gives the ability to determine the level of global correspondence between two images. During the registration process, the parameters of a given transformation model are changed, based on the optimization technique until the similarity measure reaches a maximum value of alignment [12].Hence the choice of similarity measure along with optimization method plays a crucial role to a successful outcome of a registration process.
5. II. IMAGE REGISTRATION ALGORITHM a) Medical Image Registration
In Non-rigid registration consists of Non-rigid transformations can be broadly classified by physical models or basis function expansion. While linear elasticity (Moshfeghi,1991), viscous fluid flow [13] and optical flow [14] are examples of physical model-based transformations, radial basis functions [15], multi quadrics [16], thin-plate splines [17], B-spline [18], wavelets [19] and piecewise affine transforms [20] are some of basis function expansion transformations, involves finding the optimal geometric transformation that maximizes the correspondences across the images. Medical Image Registration consists of components such as Transformation Model, Similarity Metric and Optimization Techniques as shown in Fig 1 . An image registration algorithm defines an objective function based on the similarity measure and tries to maximize this objective function. In the proposed method, a new registration method has been explained using canonical correlation analysis (CCA).
6. b) Canonical Correlation Analysis (CCA)
Canonical Correlation Analysis (CCA) can be seen as the problem of finding the basis vectors for two set of variables such that correlation between projections of the variables on these basis vectors is mutually maximized. CCA seeks a pair of linear or nonlinear transforms one for each step of variables, such that when one set of variables, is transformed, the corresponding coordinates are maximally correlated. CCA used in image retrieval, image fusion [21] and object recognition problems [22] in computer vision.
CCA finds the relationship between two multidimensional datasets [21]. The basic formulation of CCA is as follows:
For a given two multi-dimensional data sets of basis vectors or projection vectors wx, wy respectively, for two data sets that maximize the correlation between the random variables x=w x T (xi-x) and y= w y T (yi-y),
?? = ??[??,??] ???[?? 2 ]??[?? 2 ] = ??[???? ? ?? ???? ?? ???? ? ] ???? ???? ?? ???? ?? ???? ? ? ???[???? ?? ? ???? ?? ???? ? ](2.1)
?? = ???? ? ?? ?????????? ] ?? ???? ?? ??????????? ???? ?? ?????????? (2.2)C xx and C yy are the within-class covariance matrix and, C xy is the cross -covariance matrix. Maximum correlation has been found as follows.
? = argmax (W x T C xy Y T W y ) (2.3) s.t W x T C xx W x =1 and W y T C yy W y =1(2.4)The Basic formulation of CCA has the following disadvantage. 1. CCA finds the only linear relationship between two datasets. 2. Difficult to extend more than two data sets.
These problems can be addressed using the following ways. 1. A non-linear relationship between the data sets can be addressed using kernel extension of CCA [23].
Kernel CCA defines the non-linear mapping of two datasets ?: x ? ?(x) and ?: y ? ?(y) and performs the traditional CCA on transformed datasets. 2. Neural network based CCA extracts the non-linear relationship between datasets. 3. Locality preserving method based CCA also extracts a non-linear relationship between datasets.
7. III. Algorithm for Image Registration
Image Registration methods are trying to find the relationship between two images in intensity domain or feature domain. Regarding similarity measures this relationship is defined. Similarity measures can be classified in two categories (i) in all; similarity measure quantifies the spatial alignment between two images. Various intensity-based similarity measures such as sum of squared difference (SSD) [24], sum of absolute difference (SAD) [25], correlation coefficient (CC) [26], NCC [27] and ratio image uniformity (RIU) [28] have been proposed for mono modal registration process. These measures do not perform well in all cases. While SSD [25] is highly sensitive to Gaussian noise, SAD is less responsive to outliers on the subject boundaries. CC, NCC and, RIU perform well in these conditions, but are highly sensitive to non -uniform illumination in the images and (ii) The Non-linear similarity measures such as mutual information or divergence measures, etc. Multimodal image registration, the images are captured through different sensors (CT or MRI) or different parameters (T1, T2 or FLAIR) so that the intensity relationships between images are highly non-linear.
In this work, based on the structural representation of images an algorithm has been proposed. The dense set of descriptors which perform the intensity based registration replace the input images. The advantage of this method is that after new representation, one can use any simple similarity measure such as L2 norm or SSD [25] for multimodal image registration.
8. Given two images find projection directions using
Kernel CCA (Gaussian kernel used for projection). 2. Project original images or features in lower dimension space using projection direction. 3. Use L2 norm as a similarity measure.
In this algorithm Gradient descent uses ? optimization function.
9. IV. Methodology
Using two sets of experiments the work has been carried out and is detailed below 1. First set of demonstrations on T1 and T2 MR Images for 3D rigid registration (RIRE dataset). Experiments are carried out with the specifications: 15mm translation and 10-degree rotation as a deviation from correct position with ten times with different affine parameter settings. Mutual information based method for rigid registration has been used to be compared against the experimental results. We show the absolute error for translation (in mm), rotation (in degree) and root mean square error (RMS) in Tab. 1. Consider 1 mm equal to 1 degree for the absolute error computation. CCA has been performed on for more than two modalities (T1, T2, and PD) also. Tab. 2 Shows results for Brain web dataset. Comparison purpose uses the MIbased on pairwise registration framework. CCA based method performs better regarding accuracy (Tab1) (in translation and rotation) compared to MI-based method. CCA based method improves overall accuracy to 6.7% in pairwise registration and 13 % in Groupwise registration compared MI-based method. The Degree of freedom: 9 0 The work has been carried out using two sets of experiments and are detailed below. Table 1: For the error calculation, five manual points were marked on the MRI image. In the second set of images also the experiments in a similar environment and the same method are used for error calculation. Results have been shown in following Tab.4.
10. V. Results
11. a) Figures and Tables
12. Conclusion
In this work new algorithm, CCA has been proposed for image registration. In multimodal framework, due to different acquisition parameters, the relation between datasets not follows the linear relationship. In this algorithm, the kernel version of canonical correlation analysis was used because the basic formulation of CCA gives the only linear relationship between datasets. The results are shown in Table I, Table II Two sets of experiments have been performed on the RIRE datasets (T1, T2, and PD images). (i) Pair wise registration and (ii) Group-wise registration. From table I, Table II, it is evident that group-wise registration performs well compared to pairwise registration because group-wise registration consists of extra information (due to other modalities) which helps registration. The advantage of using CCA based method is one can easily extend this framework for more than two modalities.
| Method | Translation x(mm) | Translation y(mm) | Rotation (Degrees) |
| MI-based | 3.1 | 2.0 | 4.2 |
| CCA | 2.9 | 1.8 | 4.0 |
| Moving image | Static image |
| Registered Image_MI | Registered image_CCA |