Alpha Trimmed Mean based JPEG Compression for an Objective Image Quality Enhancement of Noisy and Noise Less Images

Table of contents

1. I. Introduction

he encoder generates a set of symbols when a two-dimensional image f(x, y) is given as an input. Then transmit this through a channel and the encoded image is now sent to the decoder. The decoder generates a reconstructed image f'(x, y). The output f'(x, y) is an accurate imitation of f(x, y) in lossless compression. Else it means that there is some misconception present in the re-enacted image [1].

The JPEG (Joint Photographic Experts Group), the committee that shaped the JPEG standard, is an identifiable lossy compression proposal. Not just using less memory, but also the data in the regenerated image in a JPEG compression appears very much identical. Though the quality is reduced with JPEG compression, the image will look nearly as similar as the original image.

The JPEG Algorithm wipes out high-frequency components that the human eye can't identify.

2. a) JPEG Algorithm

When compared to straight better, it involves the following steps. 1. The acquired image can be divided it into 8-pixel by 8-pixel blocks. If the image size is not precisely multiplied by 8, then add zeros in empty pixels around the edges. [1].

If in 8x8 blocks include a lot of dissimilarity in pixel values then the number of constructive DCT coefficients will grow to be more. Otherwise only first few DCT coefficients will be more noteworthy while others are zeros. On the application of filters, as a result the image gets smoothened the distinction of the pixel values of a block abridged [1].

3. II. Intended Innovative JPEG Compression Algorithms

If in 8x8 blocks include lot of distinction in pixel values then the number of constructive DCT coefficients will grow to be more. Otherwise only first few DCT coefficients will be more noteworthy while others are zeros. On the application of filters the image gets smoothened as a result the distinction of the pixel values of a block abridged.

There are two different ways to implement the JPEG Algorithm. 1) Earlier than segregating the image into 8X8 blocks the images tainted with Poisson, Speckle, Salt & Pepper noise and Gaussian noise is convoluted with Alpha trimmed Mean filter.

2) Before the application of normalized matrix, the image is convoluted with the Alpha trimmed Mean filter. This paper examines the comparison between the proposed approaches with the standard JPEG compression. The planned methods illustrate enhanced results compared to the JPEG in terms encoded bits. This paper implements the proposed algorithms by using MATLAB tools and the images are extracted from SIPI image database. Algorithm1: Alpha trimmed Mean Based JPEG algorithm on noisy images. Step1: Read the image.

Step 2: Apply the smoothening operator Alpha trimmed Mean.

Step 3: Standard Jpeg Compression [7,8,9].

4. III. Implementation of Planned JPEG Algorithms

In this paper Alpha trimmed mean based JPEG compression is executed on images of different sizes. Contemplation of results entrusts that the lately expected compression techniques are enormously a prominent alternate since they are proved to be better regarding image quality metrics like PSNR, MSE, AD, SC, Compression ratio.

N1 is the extent of information hauling units required to imply uncompressed dataset and N2 is the number of entities in the encoded dataset. The units for N1 and N2 are same. Step1: Read the image.

5. CR = N1/N2

Step 2: Apply speckle/Poisson/ Gaussian/ Salt & Pepper Noise.

Step 3: Apply Alpha trimmed Mean.

Step 4: Standard Jpeg Compression [8,9].

The reconstructed image is identical to the original image with lossless compression algorithms as they not only swab out redundancy but also eradicates the redundancy present in the data they even guard all the information that is present in the input image.

Higher compression is achieved in lossy compression algorithms as the output image and the input image will not be similar. We can either use subjective fidelity criteria or objective fidelity criteria for comparing the original and reprocessed image. An example for objective fidelity criteria is Root mean square (RMS) error.

Measurement of the image quality is an imperative implication in image processing. In many of the image processing applications, estimation is a compulsion for the excellence of the image. The judgment of the quality of an image by the human is not sufficient. Therefore some more metrics like PSNR (Peak Signal to Noise Ratio) and MSE (Mean Square Error) are needed. PSNR is one of the specialized image quality metric. The differences between the restructured image and the input image will be small when the PSNR value is high.

This paper spot the comparison between the proposed Alpha trimmed Mean based approaches with the standard JPEG compression. The premeditated approaches exemplify improved results contrasted to the JPEG. Out of these proposed JPEG compressions the Alpha Trimmed Mean filter on images corrupted with on Poisson noise in algorithm1, Alpha trimmed Mean on images encodes the images with a fewer number of bits, as a result the images will be transmitted with high speed. The decisive insinuation in image processing is the amount of image quality. Evaluation and assessing are obligatory for image quality in many image processing implementations. The refinement of human to boost the image quality is not adequate. So we necessitate some additional image quality metrics like Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR).

The number of encoded bits required to characterize the compressed image is minimized with the Alpha trimmed Mean. The corrupted images with Poisson noise in the proposed algorithm resulted a high compression ratio compared to the standard JPEG compression technique.

6. IV. Results

This paper presents the evaluation between the proposed Alpha trimmed mean based JPEG approaches with the standard JPEG compression. The wished-for approaches typify improved results compared to the JPEG. This paper makes use of MATLAB tools to access the proposed algorithm and the images are from SIPI image database.

7. Conclusion

In this paper, Alpha trimmed mean based JPEG compression algorithm is proposed. This algorithm is evaluated with standard JPEG algorithm. The proposed algorithm uses less encoded bits for compression of images and hence the loading and storing of the image took less time. Also, the mean square error (MSE) of the proposed approach is low compared to the regular classification correctness is augmented with the estimated approach. The projected compression ratio can be realized with good quality image with necessary planned algorithm compared to JPEG compression technique. The requirement of encoded bits to represent the compressed image is less compared to JPEG compression. Also the image corrupted with various types of noises like Gaussian, Poisson, Speckle, Salt & Pepper noise are compressed efficiently with alpha trimmed JPEG compression. This proposed alpha trimmed JPEG compression algorithm eliminates the noise and encodes the image with fewer number of bits compared JPEG compression technique. JPEG. Due to the peak signal noise ratio (PSNR) perfect

Figure 1. Fig. 1 :Algorithm 2 :
12Fig.1: Structure of Planned JPEG algorithms on images corrupted with various types of noise.
Figure 2. Fig. 2 :
2Fig. 2: Structure of Planned JPEG algorithms on images corrupted with various types of noise.
Figure 3. Fig. 1 :Fig. 2 :Fig. 4 :Fig. 5 :Fig. 6 :Fig . 8 :Fig. 7 :Fig. 3 :
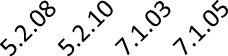
12456873Fig.1: Comparison between JPEG and Alpha trimmed mean in terms of No of bits transmitted for images of size 256×256
Figure 4.
Note: frequency components. Next, the assortment of significant 2-D normalized DCT Coefficients by traversing in a ZIGZAG fashion and categorizing them in a 1-D array. In the 1-D array, the two types of DCT coefficients the first one is termed as direct current (DC) element, while other coefficients are called alternating current (AC) elements. Variable length Huffman coding is used to code AC components. 6. The reverse operation of compression is decompression. First calculate the normalized DCT values by decoding the compressed bit stream by Huffman code. Then organize all the DCT values in the 2-D array in a ZIGZAG fashion. We can obtain the decoded DCT values by multiplying them with normalized coefficients. Now an IDCT is executed on the denormalized DCT array. The decoding process engenders ensuing image block will not be identical to respective original image block used during encoding
Figure 5. Table 1 :
1
No of Bits Required 38915 35567 40756 48505
Saved bits 485373 488721 483532 475483
RMS Error 1.99 2.14 2.16 2.95
Compression ratio 13.47 14.74 12.86 10.8
PSNR 42.19 41.55 41.48 38.76
MSE 3.96 4.58 4.66 8.71
Images 5.2.08 5.2.10 7.1.03 7.1.05
No of Bits Required 160880 185945 151629 171235
Saved bits 1936272 1911207 1945523 1925917
RMS Error 1.98 2.15 1.92 1.97
Compre ssion
ratio 13.03 11.27 13.83 12.24
PSNR 48.27 47.54 48.52 48.30
MSE 3.91 4.61 3.68 3.88
Note: © 2017 Global Journals Inc. (US)
Figure 6. Table 2 :
2
Figure 7. Table 3 :
3
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of
Bits Required 33233 32096 37968 52879
Saved bits 491055 492192 486320 471409
RMS Error 1.62 2.21 1.96 2.66
15.77 16.33 13.80 9.91
PSNR 43.95 41.28 42.30 39.67
MSE 2.64 4.88 3.86 7.07
Figure 8. Table 4 :
4
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of
Bits 131762 128052 130105 112493
Required
Saved bits 392526 396236 394183 411795
RMS Error 8.30 8.21 8.14 7.18
3.97 4.09 4.02 4.66
PSNR 29.79 29.88 29.95 31.04
MSE 68.84 67.39 66.25 51.56
Images 5.2.08 5.2.10 7.1.03 7.1.05
No of Bits Required 134461 170584 124837 151040
Saved bits RMS Error 196261 1926568 1972315 1946112 1.55 1.78 1.46 1.54 Images No of Required Bits 5.2.08 5.2.10 534501 571916 7.1.03 523400 7.1.05 543731
15.59 12.29 16.79 13.88 Saved bits 1562651 1525236 1573752 1553421
PSNR 50.37 49.17 50.87 50.45 RMS Error 8.24 8.22 8.28 8.29
MSE 2.41 3.17 2.14 2.37 3.92 3.66 4.00 3.85
PSNR 35.86 35.89 35.82 35.82
MSE 67.97 67.49 68.57 68.64
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of Bits Required 32309 27980 34650 46407
Saved bits 492249 496308 489638 477881
RMS Error 1.56 1.82 1.92 2.46
16.36 18.73 15.13 11.29
PSNR 44.33 42.96 42.50 40.35
MSE 2.42 3.31 3.69 6.04
Images 5.2.08 5.2.10 7.1.03 7.1.05
No of Bits Required 134490 170840 124478 150890
Saved bits 1962662 1926312 1972674 1946262
RMS Error 1.53 1.82 1.46 1.54
15.59 12.27 16.84 13.89
PSNR 50.52 49.00 50.90 50.44
MSE 2.33 3.30 2.13 2.37
Figure 9. Table 5 :
5
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of Bits Required 31807 28385 34746 46210
Saved bits 492481 495903 489542 478078
RMS Error 1.56 1.86 1.86 2.49
Compression 16.48 18.47 15.08 11.34
ratio
PSNR 44.28 42.76 42.78 40.22
MSE 2.44 3.47 3.46 6.22
Figure 10. Table 6 :
6
Figure 11. Table 7 :
7
Figure 12. Table 8 :
8
Figure 13. Table 9 :
9
Figure 14. Table 10 :
10
Figure 15. Table 11 :
11
C ompression
atio r
ompression C
ratio
C ompression
atio r
ompression C
atio r
C ompression
r atio
ompression C
atio r
Figure 16. Table 17 :
17
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of
Bits 29370 22971 30094 45560
Required
Saved bits 494918 501317 494194 478728
RMS Error 1.35 1.68 1.48 2.17
17.85 22.8 17.42 11.5
PSNR 45.58 43.68 44.78 41.44
MSE 1.81 2.81 2.18 4.71
Figure 17. Table 12 :
12
Figure 18. Table 13 :
13
Figure 19. Table 14 :
14
Figure 20. Table 15 :
15
Figure 21. Table 16 :
16
C ompression atio r
C ompression
atio r
C ompression
atio r
Figure 22. Table 18 :
18
Images 5.2.08 5.2.10 7.1.03 7.1.05
No of
Bits 126602 168049 115194 147353
Required
Saved bits 1970550 1929103 1981958 1949799
RMS Error 1.35 1.74 1.29 1.43
16.56 12.47 18.2 14.23
PSNR 51.57 49.37 51.97 51.05
MSE 1.83 3.03 1.67 2.06
Table 19: JPEG Compression on Images of size
256X256.
Images 5.1.09 5.1.11 5.1.12 5.1.13
No of
Bits 60840 40534 50289 65622
Required
Saved bits 463448 483754 473999 458666
RMS Error 4.25 2.26 3.04 3.6
8.61 12.93 10.42 7.98
PSNR 35.59 41.10 38.50 37.5
MSE 18.10 5.09 9.26 12.94
Figure 23. Table 20 :
20
Images 5.2.08 5.2.10 7.1.03 7.1.05
No of
Bits 246431 363397 243255 298239
Required
Saved bits 1850721 1733755 1853897 1798913
RMS Error 3.48 5.39 3.8 4.7
8.51 5.771 8.62 7.03
PSNR 43.35 39.55 42.58 40.74
MSE 12.11 29.09 14.46 22.11
1

Appendix A

  1. Edge Detection Based on Mathematical Morphology and Iterative Thresholding. Bai Xiangzhi , Zhou Fugen . IEEE International Conference on Image Processing, Nov-2006. 2 p. .
  2. Centric JPEG Compression for an Objective Image Quality Enhancement of Noisy Images. Springer, International conference on smart computing and its application PP No143, 2017. p. 152.
  3. , Ch , N B Ramesh , J V Venkateswarlu , Murthy . Filter Augmented JPEG Compressions" IJCA Dec-2012. 60 (17) p. .
  4. Image Smoothening and Morphological operators Based JPEG Compression. G Marlapalli Krishna , Prasad Srinivas , Pvgd Reddy . JATIT March 2016. 85 (3) p. .
  5. + "An Improved JPEG Compression Scheme Using Human Visual System Model. G Sreelekha , P S Sathidevi . IEEE June 2007. p. .
  6. An N-Square Approach for Reduced Complexity Non-Binary Encoding, G Srinivas , Prasad Reddy , PV G , K Gjcst , No . XI Issue XI. p. .
  7. G Srinivas , P Srinivasu , T Rao , Ch Ramesh . Harmonic and Contra Harmonic Mean,
  8. A Smoothening based JPEG Compression for an Objective Image Quality Enhancement of Regular and Noisy Images, IJAER. Marlapalli Krishna , Prasad Reddy , Pvgd , G Srinivas . P P 2016. 11 (6) p. .
  9. Very Low Bit Rate Image Coding using morphological operators and Adaptive Decompositions. Olivier Egger , Wei Li . IEEE International Conference on Image Processing, Nov-1994. 3 p. .
  10. Enhanced JPEG Compression of Documents. Ravi Prakash , Joan L Member , Mitchell , David A Fellow , Stepneski . IEEE International Conference on Image Processing, Oct-2001. 3 p. .
  11. Processing JPEG-Compressed Images and Documents. Ricardo L De Queiroz , Ieee Member . IEEE Transactions on Image Processing December 1998. 7 (12) p. .
Notes
1
© 2017 Global Journals Inc. (US)
Home 
Date: 2017 2017-01-15