1. I. Introduction
ith the increase in information technologies and associated software applications, the inevitable requirement of software reliability has alarmed scientific societies, industries as well as academician to develop certain optimal paradigm to ensure defect free software applications for long run reliability.
Furthermore, the cost factor for software products and services also suggests the defect free software solutions, so as to eliminate probability of faults in future and iterative maintenance. In order to accomplish these objectives, the efficient software defect prediction (SDP) systems are of great significance. In order to ensure optimal software reliability, the defect prediction has become an inevitable part of software development life cycle (SDLC) that intends to eliminate the probability of software failure in run time. The earlier defect prediction can enable software professional to identify fault-prone modules and thus can debug the defects to ensure quality of service provisioning. In recent years the application of open source software has increased tremendously and professional prefer to customize software modules and implement as per need. Still, these modules are prone to defect in real time scenarios, thus demanding for fault prediction and verification [1,2,3,4] before introducing product to the users. The SDP might be functional on the basis of certain software metrics [3,4,5] like changes in source code, earlier defect or fault etc. Typically, software metrics do represent certain quantitative factor that characterizes the properties of software source code, which can be employed to predict fault proneness of software during function. On the other hand, in recent years majority of software applications are being developed using Object-Oriented (OO) paradigm. The object oriented paradigm enables certain metrics that that can be employed to examine the quality of software application and associated fault proneness. Some of the predominantly proposed software metrics are MOOD [6], QMOOD [7], Bieman and Kang [8], Briand et al. [9], Etzkorn et al. [10], Halstead [11], Henderson-sellers [12], L and H metrics suite [13], McCabe [14], Tegarden et al. [15], Lorenz and Kidd [16] and CK metric suite [17]. The implementation of object oriented metrics enables software practitioners to examine quality of software in terms of precision, accuracy, fault-resilience, reliable functionality, adaptability, supportability, usability, portability, and cost effectiveness etc. In fact, it makes testing enhanced for large scale software applications. This is the matter of fact that a number of researches have been made for defect prediction. Some of the predominantly employed SDP techniques are based on machine learning and artificial neural network [18,19,20,21,22], clustering techniques, statistical method, data mining based fault identification, random forest [23,24,25] approaches etc. However, the emerging software complexities, critical software applications, reliable service assurance, quality oriented service provisioning, and cost effective or economical solutions etc., motivate researchers to develop certain cost effective defect prediction solution. In recent years, primarily, support vector machine (SVM) and artificial neural network (ANN) approaches are being explored for SDP utilities. The emergence of artificial intelligence based applications have motivated researchers to explore ANN based defect prediction that works based on the human brain functions, while encompassing multiple neurons and directed edges possessing certain weights values between input and output layers. In fact, ANN is a complex non-linear mapping process that employs output as the input for learning certain complex non-linear input-output relationship between input and output layers. In function ANN encompasses data sets to optimize key factors such as weight parameters, risk minimization mechanism for stopping training once the learning error enters in expected margin level. Although, ANN has established itself as a potential candidate for prediction and classification applications, still its limitations in terms of slow learning ability, local minima and convergence can't be ignored. In order to enhance the performance of ANN based defect prediction some researchers [26,27] have suggested evolutionary computing paradigm that could enable optimal classification and prediction without introducing any computational complexity and premature convergence.
Considering efficiency of evolutionary computing techniques such as Genetic Algorithm (GA) in this paper a robust Adaptive genetic algorithm based ANN learning algorithm has been developed, which has been used for software defect prediction. In addition, to enhance the performance of GA for huge data elements and efficient performance, the genetic parameters (crossover and mutation probability) have been selected dynamically that makes overall system much robust as compared to conventional approaches. In order to examine the performance of the proposed HENN system, a Levenberg Marquardt based ANN (LM-ANN) algorithm has been developed and the comparative performance analysis with the object oriented software metrics, CK metrics [17] has revealed that the proposed HENN algorithm provides better fault detection as compared to LM-ANN. Furthermore, the fault removal cost analysis for both the algorithms has stated that the proposed system is cost effective and can be used for real time defect prediction utilities.
The remaining sections discusses, related work in Section II, the research contributions and problem definitions for the proposed software defect prediction model are presented in III, which has been followed by proposed HENN and LM-AMM based SDP model discussion and implementation in Section IV. Section V presents the results and analysis and conclusion has been discussed in Section VI. The references used in this paper are given at the last of the manuscript.
2. II. Related Work
Software reliability is of course an inevitable need for quality service provisioning. The reliability oriented software defect prediction (SDP) has motivated researchers to develop optimal system for cost efficient defect prediction. Researchers examined the relationship between object oriented software metrics and associated faults [28,29,30,31,32,33] by means of machine learning algorithms and detected fault proneness of software. To achieve better prediction some other approaches such as decision trees, naïve Bayes, and 1-rule [34] based fault detection scheme were developed, where the standard datasets such as NASA MDP was used to examine classification accuracy of the SDP approaches. Chug et al [35] demonstrated fault identification using data mining and employed conventional J48, Random Forest, and Naive Bayesian Classifier (NBC) schemes for performance comparison but still couldn't employ the benefits of advanced classification approaches. To optimize conventional random forest based defect prediction Pushphavathi et al [36] incorporated a hybrid random forest (RF) and Fuzzy C Means (FCM) clustering model for software defect prediction. Unfortunately, these approaches could not address the issue of unbalanced datasets, which motivated researchers to come up with Adaboost. Nc [37] which implemented a number of class imbalance approaches, re-sampling, threshold variations, and ensemble algorithms. Exploring insight, this approach can be found to be complicate and not a cost effective solution for large scale dynamic data. Researchers used SVM based defect prediction scheme [38,39] and a dynamic SVM model was proposed that intended to detect faults in source code by means of error data and faulty code execution. In [40,41]an ANN based defect prediction model was developed. A defect severity model using conventional back-propagation learning based ANN was developed in [42]. Similarly in [43] a Radial Basis ANN was used for SDP. ANN based SDP for Halstead data metrics has been done in [44]. In [45] the Bayesian Regularization (BR) technique based ANN model was developed for software fault detection. Almost all ANN based defect prediction model employs conventional learning and weight estimation techniques that confines applicability with huge datasets with dynamic functional environment. The conventional learning and weight estimation approaches can't eliminate the key issues of local minima and convergence issue that limit the performance of generic ANN. The enhancement of learning scheme and further optimization through certain evolutionary computing approaches can make ANN robust for SDP applications. In fact, cost feasibility is one of the key factors that decide employability of certain SDP model, but till no any research work has addressed the issue of cost estimation of the defect prediction model. This paper has considered these limitations as motivation and has developed an evolutionary computing A-GA based SDP model which has been compared with Levenberg Marquardt based ANN and respective fault removal cost estimation has been done.
3. III.
4. Our Contribution
In SDLC the fault resilience and reliability is of great significance. The implementation of efficient SDP strengthensearly fault detection and thus it enables software practitioner to remove faults to ensure reliability and QoS of the software solution. The predominant question in this paper is whether the implementation of Adaptive Genetic Algorithm can enable efficient and cost effective SDP solutions? In this paper, object oriented software metrics [17] has been considered for defect prediction and using proposed SDP models, the fault proneness of metrics data has been retrieved, whether the data is faulty or non-faulty. In order to perform classification of faulty and non-faulty data, initially the conventional ANN learning scheme with Leven berg Marquardt (LM) algorithm [45] has been developed and respective performance towards software defect prediction with NASA defect datasets has been done. This is the matter of fact that LM based ANN performs better as compared to other approaches such as back-propagation or feed-forward learning based NN, still it suffers due to prime limitations of ANN, such as local minima and weight update issues. Thus, considering higher employability of artificial intelligence techniques and respective limitations for critical software applications, in this paper an evolutionary computing based optimization scheme called Genetic Algorithm has been used for weight estimation during ANN learning. Further to ensure optimal performance of GA, in this paper a novelty has been introduced in terms of adaptive GA parameter (Crossover and Mutation probability) selection. The proposed Adaptive Genetic Algorithm (A-GA) performs adaptive weight estimation and learning optimization so as to ensure optimal fault classification and accuracy. The A-GA optimization scheme alleviates the issue of premature convergence and local minima. Such enhancement has lead better classification and accuracy for fault detection in huge datasets.
In order to examine the performance of the proposed SDP model, the object oriented software metrics (here, CK metrics [17]) has been considered. The implemented metrics characterizes various software features. In this paper, six predominant software metrics have been considered in fault identification. The considered metrics are WMC, NOC, DIT, CBO, RFC, and LCOM. The individual metrics has been feed as the input of the ANN and performing learning with the proposed HENN model the classification for faults has been done. The discussion of the proposed A-GA based ANN (HENN) has been discussed in the next section of the presented manuscript. In this paper, in order to examine the cost effectiveness of the developed SDP models, certain cost efficiency model can be used [46, 47, and 48] and with certain standard threshold the applicability of the proposed SDP model for large scale software data can be examined. The performance analysis of the proposed model has been done in terms of accuracy, precision, recall, F-Measures and fault removal cost efficiency. The discussion of the proposed SDP models and its implementation is discussed in the following sections.
5. IV.
6. System Model
In this section, the proposed Levenberg Marquardt learning based ANN and our proposed HENN based software defect prediction schemes and its algorithmic implementation have been discussed.
7. a) Artificial Neural Network based Software Defect
Prediction This is the matter of fact that the Artificial Neural networks (NN) have seen an explosion of interest over the years, and it has been implemented across a range of problem domains, specifically classification and prediction. In fact, the major problems dealing with prediction and classification, ANN is considered to be the dominating solution. For SDP scenario, ANN can be used with different learning schemes like Gradient Descent (GD), Gauss Newton, and Levenberg Marquardt (LM) etc. Unfortunately majority of existing learning paradigm are ineffective to alleviate the key limitations of ANN such as local minima and convergence issue. Even though, researches have revealed that Levenberg Marquardt (LM) can be a potential candidate for ANN learning due to its stable nature and flexible implementation. In this paper, in addition to LM-ANN algorithm, an evolutionary computing technique called Adaptive Genetic Algorithm (A-GA) has been used for dynamic weight estimation for prediction enhancement. In the proposed ANN model and ultimately intended SDP system, it has been intended to find relation between object oriented software metrics and fault prone classes of the six CK metrics; WMC, NOC, DIT, RFC, CBO, LCOM, which has been considered as independent variable. The fault data has been taken as the dependent data. Figure -1 illustrates the architecture of our proposed ANN model comprising three layers i.e., input layer, hidden layer and output layer. Here, 6 input nodes have been defined that takes six CK matrix [17] having multiple classes as individual input. Since, in the proposed ANN model, the expected outputs are either FAULTY or NO-FAULTY, therefore only one output node is needed. Here, we have considered 8 hidden layers so as to avoid unwanted computational complexity. Thus in the defined Generally, the ANN model is defined in terms of a function?? ? = ð??"ð??"(??, ??)where ???states for the output vector and?? and ??represent the weight vector and the input vector respectively. In learning process, the weight factor ??is updated iteratively so as to minimize the Root Mean Square Error (RMSE), which can be estimated by:
?????? = 1 ?? ???? ?? ? ? ?? ?? ? 2 ?? ??=1(3)Where ??depicts the actual output and?? ?? ? represents the expected output.
In order to make computation efficient and to process multidimensional data with ANN, it is inevitable to perform the normalization. In the proposed ANN based SDP models; the data normalization has been done using Min-Max approach, which is discussed as follows:
i. Data normalization In this paper, normalization has been performed on the defect datasets that strengthens the proposed ANN based software detect prediction systems for better readability and classification. In the proposed SDP model, the data normalization has been done over the range of [0, 1] so as to adjust the defined range of input feature value and avoid the saturation of neurons. There a number of normalization approaches such as Min-Max normalization, Z-Score normalization and decimal scaling etc. We have normalized the defect data using Min-Max normalization scheme that performs a linear transformation on the original data and then maps individual data ?? ?? of attribute ?? to the normalized value ??? ?? in the range of [0, 1]. The normalization using Min-Max approach has been done using following equation:
????????????????????(?? ?? ) = ?? ?? " = ?? ?? ? ?????? (??) ??????(??) ? ?????? (??)(4)where ??????(??) and ??????(??) are the maximum and minimum values of the attribute ?? respectively. In the proposed SDP model, performing data normalization the ANN model has been implemented for fault classification.
In ANN based systems, the efficient weight estimation and learning approach is of great significance. Till a number of approaches have been developed for learning optimization in ANN based artificial intelligence applications. Some of the predominant approaches are: Gauss Newton, Gradient descent, Levenberg Marquardt (LM) etc. Interestingly LM can work as both gradient descent as well as gauss Newton. Some researchers also have advocated that LM can outperform other existing learning schemes in ANN. Thus considering significance of LM for effective learning for SDP, in this paper initially LM based ANN (LMANN) has been developed for SDP model. The discussion of the proposed LMANN model for SDP application is given as follows:
8. b) Levenberg Marquardt (LM) Learning based ANN for Software Defect Prediction
The prime scope for ANN optimization is the enhancement of its weight estimation and respective learning optimization. Therefore, considering these factors, a number of algorithms have been proposed for weight update in ANN learning (Table - Levenberg Marquardt (M) algorithm performs localization of the bare minimum value of multivariate function in a repetitive manner, which is expressed as the sum of squares of non-linear real-valued functions. Similar to GD algorithm, in HENN, LM algorithm updates the weights during NN learning process. Considering the performance novelty, the proposed LM algorithm comprises the functional ability of Steepest Descent and Gauss Newton method. The proposed LM algorithm can update the weight vector by following expression:
?? ??+1 = ?? ?? ? (?? ?? ?? ?? ?? + ????) ?1 ?? ?? ?? ??(1)Where W k+1 is the updated weights, W k is the current weights, I represents the identity or unit matrix, ?? is the Jacobian matrix andµ, the combination coefficient is always positive. With µ as very small, it functions as Gauss Newton method while making µ as very large makes it functional as Gradient descent method. The Jacobian matrix derived as given as:
?? = ? ? ? ? ? ? ? ? ?? ???? 1 (?? 1,1 ) ?? ???? 2 (?? 1,1 ) ? ?? ???? ?? (?? 1,1 ) ?? ???? 1 (?? 1,2 ) ?? ???? 2 (?? 1,2 ) ? ?? ???? ?? (?? 1,2 ) ? ? ? ? ?? ???? 1 (?? ??,?? ) ?? ???? 2 (?? ??,?? ) ? ?? ???? ?? (?? ??,?? ) ? ? ? ? ? ? ? ? (2)Where ?? refers the weight counts and the input patterns are P. The output patterns are indicated by ??. In the proposed SDP model, in the initial phase the LM algorithm has been used to estimate the weights for the learning scheme. Figure 3 represents the adaptive weight estimation approach using LM algorithm. The weights are updated dynamically so as to reduce RMSE and satisfying the stopping criteria, the classification has been done for fault prediction. On the basis of fault classification, the confusion matrix has been obtained which has been employed further to examine performance of the proposed SDP model. This is the matter of fact that LM-ANN has been employed for varied classification utilities but considering the specific requirements of fault prediction and robust function with huge data sets in real time software utilities, the local minima problem and convergence issues of ANN can't be ignored. Thus, considering these limitations, in this paper, the evolutionary algorithm Adaptive-Genetic Algorithm (A-GA) has been used for parameter optimization that can strengthen the function of the proposed system to yield more precise, accurate and efficient outputs. The implementation of A-GA for ANN based SDP utility has been discussed in the following section
9. c) HENN: Hybrid Evolutionary Computing Based Neural Network for Software Defect Prediction
In recent years a number of optimization schemes have been developed on the basis of the concept of human evolution and Genetic Algorithm (GA) is one of the predominant one. GA is an adaptive search approach based on the evolutionary concepts of natural selection that intends to find certain optimal or near optimal solutions. In fact, the basic concept of GA is based on the philosophy of natural selection and Darwin principle of the survival of fittest. In function, GA at first performs random population generation, where population represents certain set of solutions. In fact, these solutions are nothing else but a chromosome possessing a form of binary strings where all the comprising parameters are supposed to be encoded. Performing population generation, GA calculates the fitness value, also known as fitness function for the individual chromosome. The fitness value represents a user-defined function that provides the estimation results for individual chromosome, and thus a higher fitness value signifies the chromosome to be the dominant one. On the basis of retrieved fitness values, the offspring are generated by means of genetic operators called crossover and mutation. Implementing genetic operators the population generation continues until the stopping criteria is achieved. Here, it must be noted that after every generation, chromosomes having fitness value more than defined threshold are considered for next generation otherwise are mutated out of competition.
As depicted in Figure -1, the developed HENN model [59] encompasses ?? ? ? ? ?? network configuration having?? input layer, ? hidden layer and ?? output layer or nodes. In the proposed ANN model, all the six CK metrics under consideration have been fed as input to the individual input nodes, where the individual metrics can have multiple classes depending on the size of software and dimensions. As already discussed with the considered 6-8-1 ANN configuration, the total number of weights, N to be calculated are:
?? = (?? + ??) * ?(5)In the proposed model the individual weight is considered as a gene in the chromosomes and is a real number. Consider??, the gene length or the number of digits be??, then the length of the chromosome ?? ????????? can be obtained using following equation:
?? ????????? = ?? * ?? = (?? + ??) * ? * ??(6)In the proposed A-GA based scheme all chromosomes are considered as the population and for each chromosomes the fitness values and weights are estimated. In our proposed model, the weights (?? ?? ) has been obtained using following equation:
?? ?? = ? ? ? ? ? ? ? ??ð??"ð??" 0 ? ?? ???? +1 < 5 ? ?? ???? +2 * 10 ???2 + ?? ???? +3 * 10 ???3 + ? + ?? (??+1)?? 10 ???2 ??ð??"ð??" 5 <= ?? ???? +?? <= 9 + ?? ???? +2 * 10 ???2 + ?? ???? +3 * 10 ???3 + ? + ?? (??+1)?? 10 ???2(7)To perform A-GA based weight estimation in ANN, the fitness values for individual chromoseomes are needed to be obtained. The algorithm developed for fitness value estimation is given in the following figure
?? ?? = 1 ?? ?? = 1 ? ? ?? ?? ?? =?? ?? =1?? Figure 3 : Fitness generation using A-GA Genetic algorithm (GA) has been considered as a potential global optimization approach for major applications; still this approach can be further optimized to alleviate issues of premature convergence. In this paper, in order to alleviate these issues, the genetic parameters, cross over probability (?? ?? ) and mutation probability (?? ?? ) has been selected dynamically so as to get optimal or sub-optimal solution efficiently without converging. To update ?? ?? and ?? ?? the following mathematical equations has been used:
(?? ?? ) ??+1 = (?? ?? ) ?? ? ?? 1 * ??5(?? ?? ) ??+1 = (?? ?? ) ?? ? ?? 2 * ?? 5(8)where The overall discussion of the proposed HENN model is given as follows:
(10. ? HENN-SDP Simulation
Since, the proposed HENN model operates on the basis of genetic algorithm principle; it also encompasses processes such as, population generation, selection, crossover, fitness estimation, and mutation. A brief discussion of the implemented HENN simulation model is given as follows:
Step-1 Population Initialization: In our model randomly 50 chromosomes are selected randomly to perform competition. These randomly selected chromosomes perform crossover with defined crossover and mutation probability.
Step-2 Weight Estimation: HENN estimates weight ?? ?? for each selected chromosomes as input to the hidden layer and hidden layer to the output layer using equation (7).
Step-3 Fitness Estimation: On the basis of weight estimated, the fitness value is obtained for individual chromosome with an intention to minimize the root mean square error (RMSE) obtained at the output node of ANN.
Step-4 Chromosome Ranking and Mutation: On the basis of fitness values for the individual chromosomes, the ranking is performed which is followed by mutation of the chromosomes having lower fitness values and chromosomes with higher ranking replaces chromosomes with lower fitness.
Step-5 Crossover: In the proposed HENN model, the two point crossover is performed with the selected chromosomes. Here to enhance computational efficiency the GA parameters, ?? ?? and ?? ?? are varied adaptively, as per equation (6). Initially, ?? ?? and ?? ?? have been assigned as 0.6 and 0.1 respectively and ??refers the number of chromosome having similar fitness value.
? Stopping Criteria: The process of weight estimation using HENN algorithm continues till the stopping criteria is not achieved and the 95% chromosomes in gene pool achieves unique fitness value, as beyond it the fitness level of chromosomes get saturated.
Step 6 Fault Classification: Considering step-3, and stopping criteria, with the optimal RMSE, the final output at output layer of ANN is obtained that more than 0.5 signifies towards FAULTY class otherwise NON-FAULTY.
Step 7 Confusion Matrix: On the basis of FAULTY and NON-FAULTY label of comprising classes, a Confusion Matrix is derived that is used for performance evaluation. Thus, implementing the above mentioned approaches, the proposed HENN model performs Software Defect Prediction. This is the matter of fact that a number of SDP systems have been developed but only prediction accuracy and precision can't be the justification for a system to be employable in real time scenarios. Industries demands for certain cost effective and efficient system for defect prediction. A system with higher computational efficiency with minimal cost of fault detection and removal can be of great significance and can be suggested to be used in real time SDP applications.
Thus, considering the need of a novel cost analysis mechanism, in this paper a novel cost estimation approach has been developed which has been used to assess the computational (Fault detection and removal) cost analysis for both our proposed HENN based SDP as well as reference, LM-ANN based SDP model. The discussion of the proposed cost estimation model is given as follows:
11. d) Software Fault Estimation and Removal Cost analysis
In this paper, a novel cost estimation approach has been developed that estimates the cost of fault detection and removal, as the efficiency to be considered as a criterion that decides whether the system should be used or not in real time applications. The proposed cost estimation model has been derived from [46]. In the developed cost estimation approach, certain constraints have been assumed such as, varied testing phases might take different cost for certain fault removal as different softwares are developed in varied software platform and with varied development standards, and it is impractical to perform comprising unit testing on all the associated modules [47]. In the proposed cost estimation model, the identification efficiency model proposed in [48] has been incorporated that suggests following efficiencies to be used for cost estimation model. In this paper, the following notations have been used to formulate mathematical model for fault estimation and removal cost.
Cost Norm = ???????? ???????? _?????? ???????? ???????? _???????? = ? < 1, ????ð??"ð??"????ð??"ð??"?????????? ?????? ???????????? ? 1 Not Suitable(11)Here, Cost Estm SDP represents the estimated fault removal cost for software with fault prediction scheme, Cost Estm _WSDP is the fault removal cost without using any SDP system. The variable Cost Norm refers the normalized cost with the SDP models. As illustrated in above expression, the minimal normalized cost signifies better employability of a defect prediction system. In this paper, the cost analysis for both the proposed HENN as well as Levenberg Marquardt based ANN (LMANN) has been done. The results obtained are given in Table 7.
V.
12. Result and Analysis
This section discusses the experimental setup, benchmark fault data, results and performance analysis.
In this paper, the overall algorithms for artificial neural network, Levenberg Marquardt based ANN, Adaptive Genetic Algorithm and its implementation with ANN for defect prediction, etc have been developed using MATLAB2012b software model. In addition, the toolboxes of machine learning and artificial neural network have been considered to perform simulation. In order to examine the performance of the proposed HENN model, object oriented software metrics suite, CK Metrics [17] has been considered, which has been derived from the fault data taken from PROMISE [49] and NASA MDP [50] fault data repository. The software metrics from the fault datasets (JEdit, Ant, Camel and IVY)have been derived using Chidamber and Kemerer Java Metrics tool (CKJM) tool that extracts software metrics by executing byte code of compiled Java cases and assigns a definite weight of the comprising classes having feature vectors. In this paper, six predominant CK metrics have been considered as depicted in the Table-4. A set of approaches that can be executed in response to a message received by an object of that class LCOM Dissimilarity measurement of varied methods in a class using instanced attributes/variables In our work, the six software metrics have been considered as the independent data while the fault data has been taken as dependent variable.
The considered data JEdit, Ant, Camel and IVY comprise static code measures along with varied modules sizes, defective modules and defect rates. In the proposed SDP models the respective extracted weights and features of the data classes have been taken as input to the ANN as illustrated in Figure -1. On the basis of final outcome of the both SDP models, LM-ANN as well as HENN for individual datasets, the confusion matrix has been obtained. A confusion matrix comprises two rows and columns representingtrue positive (TP), false negatives (FN), false positive (FP) and true Negative variables. The variables in confusion matrix represent the faulty and non-faulty data and its severity. As depicted in Table-5, TP depicts modules which are classified as FAULTY, FN represents the modules which are FAULTY but are classified incorrectly as NON-FAULTY. Similarly, FP represents the modules which are non-faulty but are classified as faulty.
13. a) Result Analysis
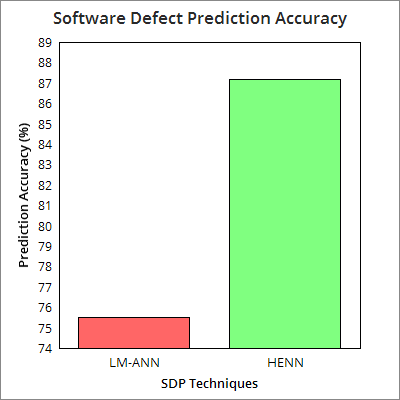
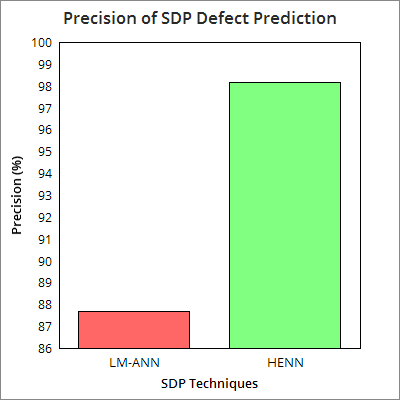
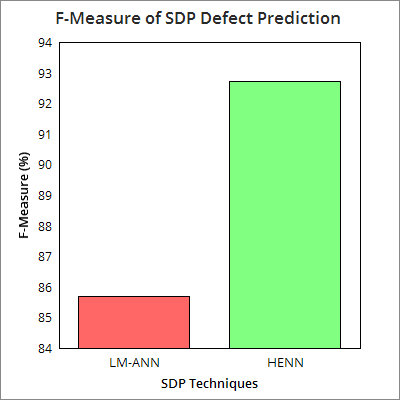
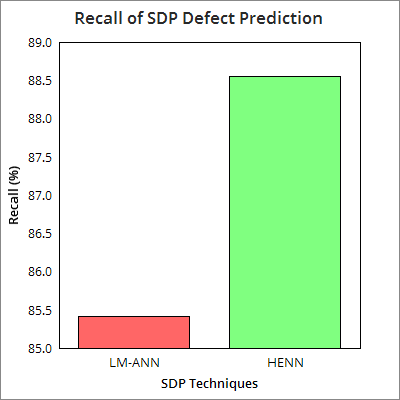
The following section represents the results obtained from the proposed HENN based SDP model and a reference model based on Leven berg Marquardt based ANN. Here, from the results obtained it can be found that the proposed HENN based SDP model performs better than Leven berg Marquardt algorithm based ANN (LMANN). Here, it can be found that the average fault prediction accuracy of the proposed HENN model is 87.23%, on contrary, the LM-ANN based SDP models delivers 75.48% and hence the proposed system outperforms the existing and till most efficient ANN model, LMANN. In addition, the analysis results states that the proposed system provides 98.2% precision, 92.74% F-measure, 88.55% of recall, which is 87.7% 85.7%, and 85.4% for LMANN based SDP system, respectively. The following figures (Figure 5-8) represent the average performance of the proposed system with four benchmark datasets (JEdit, Ant, Camel and IVY). The performance results for the developed SDP models with individual datasets are given in Table-7. Considering cost effectiveness of HENN and LMANN based SDP models, Figure 9 depicts that the proposed HENN based system is most cost efficient as compared to LMAMM, and hence it can be implemented for real time applications intending software defect prediction and removal. 7 depicts that the proposed defect prediction approach is highly robust and efficient as compared to Levenberg-Marquardt based ANN system, which is supposed to be the most effective ANN system till. The proposed HENN model has exhibited better cost effectiveness for the fault detection and removal than LMANN. Further to explore effectiveness of the proposed HENN model as compared to other existing systems, a comparison has been done (Table -8) and results revealed that the proposed system can be the best optimal solution for defect prediction for object oriented software applications. [57] 94.2 --Symbolic Regression [57] 89.50 --RBP-NN [57] 80.0 --LP [52] 86.6 86.6 87.4 Naive Based [52] 85.6 83.1 83.9 CPSO [53] 69.2 67.6 -T-SVM [54] 75.8 84.1 80.9 GANN [53] 73.4 81.6 -AdaBoost [53] 79.1 82.3 -Random Forest [58] 91.4 -k-NN [56] 91.8 --C4.5 [56] 88. J 48 [56] 90.9 Levenberg-Marquardt-NN [56] 88.0 --NNEP-Evolutionary [53] 88.8 81.2 -PSO [55] 78.7 --PSO-NN [57] 97.7 --HENN SDP 97.9 1 98.9
VI.
14. Conclusion
In order to ensure optimal software reliability and quality of service the earlier prediction of faults and its removal is of great significance. In addition, the cost effective solution for defect prediction and fault removal has motivated industries as well as academician to develop a novel SDP solution that could ensure cost effective and optimal defect prediction solutions. In this paper, an object oriented software matrix based defect prediction model has been developed.
Considering the limitations of artificial intelligence techniques such as artificial neural network, in this paper an evolutionary computing technique named Adaptive Genetic Algorithm (A-GA) has been developed for ANN dynamic weight estimation and learning optimization. The proposed Hybrid Evolutionary computing based Neural Network (HENN) based system has been employed for SDP system. Furthermore, Levenberg Marquardt algorithm based ANN algorithm (LMANN) has been developed for defect prediction. Considering cost effectiveness of the defect prediction systems, a novel mathematical model has been derived and the cost analysis results confirms that the proposed HENN model is cost effective as well as performs better as compared to other existing systems. The simulation results obtained with PROMISE and NASA MDP datasets exhibits that the proposed model performs on average 87.23% accuracy and the best classification accuracy obtained is 97.99% with 100% precision. The proposed model delivers 98.97% of Fmeasure. The cost analysis exhibits that the proposed HENN model is approximate 21.66% cost effective as compared to LMANN. The comparative analysis in this paper reveals that the proposed HENN model performs better as compared to other existing techniques. This paper could perform cost analysis of only HENN and LMANN, hence in future other defect prediction models can also be examined for their cost effectiveness for real time applications.
15. Global Journal of C omp uter S cience and T echnology
Volume XV Issue II Version I Year ( )

| 1). In this paper, |
| Algorithm for Fitness Estimation | ||||
| Input:?? ? | ||||
| ?? ?? = | ? ? ? ? ? ? ? ? + | ??ð??"ð??" 0 ? ?? ???? +1 < 5 ?? ???? +2 * 10 ???2 + ?? ???? +3 * 10 ???3 + ? + ?? (??+1)?? 10 ???2 ??ð??"ð??" 5 <= ?? ???? +?? <= 9 ?? ???? +2 * 10 ???2 + ?? ???? +3 * 10 ???3 + ? + ?? (??+1)?? 10 ???2 | ||
| Phase-4: Calculate RMSE of chromosome?? ?? | ||||
| ?? ?? = ? | ? ?? =?? ?? =1 ?? | ?? ?? | ||
| Where ?? is the number of training data | ||||
| Phase-5: Calculate the fitness value for chromosome?? ?? | ||||
| Generate Random Population of | |||
| 'n=50' genes or Chrosomes | |||
| Extract the Weight of each chromosomes | Fed the Weight values for training in HENN model | ||
| Estimate the Fitness value for | |||
| Perform Crossover | each chrosomes | Year | |
| Replace the Minimum Fitness value Chromosome by Maximum fitness value Chromosome | No | Is threshold meet? (If Stop Criteria is accomplished. Implement the Model for Software Defect Prediction Yes | Volume XV Issue II Version I |
| ( ) G | |||
| Global Journal of C omp uter S cience and T echnology |
| Testing | Min | Max | Median |
| Unit | 1.5 | 6 | 2.5 |
| System | 2.82 | 8.37 | 6.2 |
| Field | 3.9 | 27.24 | 27 |
| Year | ||
| Volume XV Issue II Version I | ||
| ( ) G | ||
| Cost Estm _SDP | Estimated fault removal cost of the | |
| software when fault prediction is performed Cost Estm _WSDP Estimated fault removal cost of the software without using fault prediction approach Cost Norm Normalized Estimated fault removal cost of the software when fault prediction is utilized C i Initial setup cost of used fault-prediction technique C u Normalized fault removal cost in unit testing C S Normalized fault removal cost in system testing C f Normalized fault removal cost in testing M p percentage of classes unit tested FP Number of false positive FN Number of false negative | Global Journal of C omp uter S cience and T echnology | |
| TP | Number of true positive | |
| TN | Number of true negative | |
| TC | Total number of classes | |
| FC | Total number of faulty classes | |
| ? u | Fault identification efficiency of unit testing | |
| ? s | Fault identification efficiency of system | |
| testing | ||
| WMC Overall complexities of the methods in comprising classes | |
| NOC Number of sub-classes subordinate to a class in the class hierarchy | |
| DIT | Maximum height of the class hierarchy |
| CBO Number of other classes to which it is | |
| allied with | |
| RFC | |
| Predicted | Predicted | |
| Defective | Defect Free | |
| FAULTY | True Positive | False Negative |
| NON-FAULTY | False Positive | True Negative |
| In this paper, the performance of the proposed | ||
| HENN as well as LM-ANN SDP models has been | ||
| examined in terms of fault prediction accuracy, | ||
| precision, F-measure, recall, specification and fault | ||
| detection and removal cost. The mathematical | ||
| expression for considered performance parameters are | ||
| given in Table-6. | ||
| Construct | Mathematical Expression |
| Recall | ????/(???? + ????) |
| Precision | ????/(???? + ????) |
| Specification | ????/(???? + ????) |
| F-measure Accuracy | ????????????. ?????????????????? ???????????? + ?????????????????? (???? + ????)/(???? + ???? + ???? + ????) 2. |
| SDP Techniques | Accuracy | Precision | F-Measure |
| (%) | (%) | (%) | |
| LLE-SVM[51] | 81.1 | 82.5 | 80.4 |
| SVM [51] | 69.4 | 68.1 | 69.7 |
| SVM [52] | 55.3 | 88.0 | 83.2 |
| Natural Gas |
| Figure -9 : Data Modules Tech. Accuracy | Precision F-Measure | Recall | Specification | Norm. Fault | ||||
| Removal Cost | ||||||||
| (Norm.) | ||||||||
| JEDIT | 492 | HENN | 0.9799 | 1 | 0.9897 | 1 | 0.9756 | 0.2406 |
| LMANN | 0.8394 | 0.8503 | 0.9119 | 0.9832 | 0.0526 | 0.2927 | ||
| ANT | 744 | HENN | 0.8145 | 0.9343 | 0.8867 | 0.8438 | 0.6346 | 0.9149 |
| LMANN | 0.7675 | 0.9879 | 0.8684 | 0.7748 | 0 | 0.9763 | ||
| IVY | 352 | HENN | 0.8835 | 0.9936 | 0.9380 | 0.8883 | 0.3333 | 0.7115 |
| LMANN | 0.6278 | 0.6955 | 0.7681 | 0.8577 | 0.0404 | 0.8936 | ||
| CAMEL | 965 | HENN | 0.8114 | 1 | 0.8952 | 0.8102 | 1 | 0.8771 |
| LMANN | 0.7845 | 0.9743 | 0.8792 | 0.8011 | 0 | 1.3401 | ||
| 3 | - | - | ||||||