1. An Enhanced Wavelet based Image Compression Technique
Abstract-With the fast expansion of multimedia technologies, the compression of multimedia data has become an important aspect. Image compression is important for efficient storage and transmission of images. The limitation in bandwidth of wireless channels has made data compression a necessity. Wireless channels are bandwidth limited and due to this constraint of wireless channels, progressive image transmission has gained much popularity and acceptance.
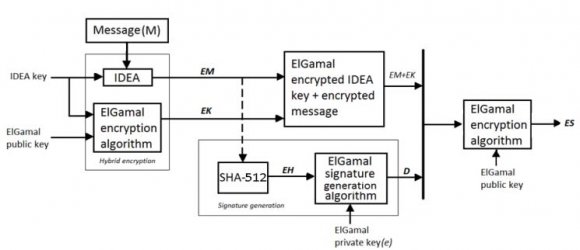
The Embedded Zerotree Wavelet algorithm (EZW) is based on progressive encoding, in which bits in the bit stream are generated in order of importance. The EZW algorithm, code all the frequency band of wavelet coefficients as the same importance without considering the amount of information in each frequency band. This paper presents an enhanced wavelet based approach to overcome the limitation of the Embedded Zerotree Wavelet (EZW) algorithm. This method divides the image into some sub-blocks. The sub image with low frequency, containing higher amount of information is compressed lossless by DPCM method, and the modified EZW (MEZW) coding and Run Length Encoding (RLE) methods are used to compress the sub-images with high frequency. Higher information part is compressed by a lossless method can result in the improved PSNR. The high frequency content of the image is less important, compressed using lossy method MEZW. The Modified EZW algorithm generates less Zerotree root symbol (Z) in comparing to EZW. Run Length Encoding (RLE) is used, to use the correlation in the coded symbols. This method can ensure that makes the best use of the hierarchical relationship of wavelet coefficients and can also improve the PSNR.
2. Introduction
ooking back through the previous years, we can see the marvelous advancement in digital media. This kind of environment gives birth to attractive applications in multimedia. Fast and instant availability of images shows the achievements of technology in the field of multimedia. Data compression is necessary in every field where data travels across the network. Today's massive use of images, generates a significant volume of data. It is required to compress these digital images, so that their transmission and storage can be simplified. Techniques to compress the image can be lossy and lossless. Lossless techniques reconstruct the actual image at the receiver side, i.e. no loss of the information. Lossless compression [21] is required in medical images, technical writing or in clip arts. The second technique is the lossy one. In this, the image at receiver side is not the same as sender side. There is always some loss of information. Lossy compression tends to increase the compression ratio while somehow compromising the quality of the image.
For still image compression, popular and well adapted algorithm is JPEG [17] standard. Similarly, MPEG [18] standard is used for video compression. Both JPEG and MPEG make use of transform coding, i.e. DCT [8] Discrete Transform. In this type of transforming only spatial correlation of the pixels inside the single 2D block is considered and the correlation from the pixels of neighboring blocks is neglected. It is extremely difficult to décor relate the blocks at their boundaries using DCT. Undesirable blocking artifacts affect the reconstructed images of video frames.
An alternative of DCT is Discrete Wavelet Transform (DWT) [1]. This wavelet transform is able to remove the artifacts of DCT and still producing the compression ratios compatible to DCT.
Wavelets are being used in many compression algorithms. Most widely used wavelet based image compression algorithms are Shapiro's EZW [2], SPIHT (Set Partitioning in Hierarchical Trees) [11], SPECK (Set Partitioning Embedded Block) [19]. These algorithms which are based on embedded coding create an embedded binary flow, a progressive data transmission that allows the image to be reconstructed using various compression ratios, allowing the algorithm to be either lossy or lossless [20].
Several modifications of Shapiro's EZW [2] algorithm have been proposed till now. The authors in [9], gives some improvements in the implementation, they used four symbols, different than the original EZW [2]. In [10], the same coefficients used by [9] and compression scheme adopted for video compression are proposed. In [12], a degree-k model, in order to quantify the coding power of zero trees in wavelet based image coding is introduced, [12] deduced that the EZW [2] is degree 0 zero tree and the SPIHT is degree 2 zero tree. It is concluded that the higher degree zero tree coder is more powerful. In [3], author presents a modification of EZW [2] algorithm. It uses six symbols to encode the wavelet coefficients instead of four symbols, which are used in the original one. It further includes binary regrouping of elements to optimize the coding.
3. Naveen Choudhary ? & Teena Hadpawat
? Following the inspiration from [2], the principle of the Shapiro algorithm is reviewed (Sect. 2). In Sect. 3, the Modified EZW (MEZW) [3] algorithm is described in detail. In Sect. 4, the proposed algorithm is described in detail. In Sect. 5, results obtained with the proposed algorithm are analyzed and compared with results from MEZW [3] algorithm and DPCM [5] algorithm. II.
4. Shapiro's Ezw Algorithm
The Embedded Zero tree Wavelet (EZW) [2] algorithm is based on embedded encoding. Embedded encoding is also called as progressive encoding. This means that when more bits are added to the bit stream, the image will contain more detail. The EZW algorithm uses embedded encoder, an embedded encoder can terminate the encoding at any point, thereby allowing a target rate or target accuracy to be met exactly. The EZW algorithm [2] has the following features. 1. Discrete wavelet transform [1] 2. Zero tree coding of wavelet coefficients 3. Successive-approximation quantization (SAQ) 4. Adaptive arithmetic coding [14] The EZW encoder is based on these two important observations: 1. Natural images in general have a low pass spectrum. When an image is wavelet transform, the energy in the sub-bands decreases with the scale goes lower (low scale means high resolution), so the wavelet coefficient will, on average, be smaller in the lower levels than in the higher levels. 2. Large wavelet coefficients are more important than small wavelet coefficients. These two observations are utilized by encoding the wavelet coefficients in several passes as EZW algorithm is a multiple pass algorithm. For every pass or iteration a threshold is chosen against which significance of all the wavelet coefficients is measured. Shapiro's encoder exploited possible dependence protocols between the different sub bands in order to create the zero trees. A zero tree is a data structure, composed of a parent and its descendants. In zero tree, for each parent at the scale i, there are four descendents at scale i-1 (Fig. 1). To make the "zero tree" effective, the wavelet coefficients are scanned for the path presented in Fig. 2. No child node is scanned before its parent node. Coding of wavelet coefficients is performed by determining the two lists of coefficients, i.e. dominant pass list and a subordinate list (fig. 4). Let us consider the matrix test (Fig. 3) in terms of the steps of EZW algorithm [2]. The wavelet transform is applied to the image and initial threshold is calculated. T o , the initial threshold is calculated using ( )
max 2 0 log 2 c T =Where c max is a maximum wavelet coefficient. For the test matrix, in fig. 3, initial threshold calculated is 32 and c max is 63.
5. b) Significance Test
The wavelet coefficients are scanned for the path presented in Fig. 2. Each coefficient is assigned a significance symbol (P, N, Z or T), by comparing each coefficient with the actual thres hold j T , where j is the iteration count):
? P (Positive and Significant): If a coefficient is greater than the threshold then it is called significant. If the sign of the significant coefficient is positive, then this coefficient will be coded as P. This is the case for the coefficients {63, 49 and 47} in the matrix test (Fig. 3)
? N (Negative and Significant): If a coefficient is significant with a negative sign, then it is coded with N symbol. This is the case for the coefficient { ?34} in the matrix test (Fig. 3).
? T (Zero tree): If the coefficient is insignificant and has only insignificant descendants. Like coefficient {24} in matrix test. The descendants of this type of coefficients will not be coded.
? Z (Isolated Zero): The coefficient is insignificant but has some significant descendants then it is coded isolated zero Z symbol. This is the case for the coefficients {-31 and 14} (Fig. 3).
The dominant list D contains information concerning the significance of coefficients, which will be coded using arithmetic coding. The significant list S contains the amplitude values of the significant coefficients, which will undergo uniform scalar quantization followed by arithmetic coding.
6. c) Successive Approximation Quantization and Refinement
The significant values {63,-34,49 and 47} from the matrix test (fig. 3) are quantized by the bits "1 0 1 0" [2]. Then, step B of the algorithm is repeated by incrementing j by 1 and dividing threshold by 2. This process is reiterated until the desired quality of the reconstructed image is reached orbit budget is exhausted. [2].
7. III.
8. Modified Ezw [3]
A modified version of traditional Embedded Zero tree Wavelet encoding names MEZW [3]. In general [3] modified the EZW [2] in the following manner: 1. Symbols were added in the significance test step (step B). More symbols allow a better redistribution of the entropy. 2. Coding of the dominant list D elements and subordinate list S quantization bits was optimized by the binary regrouping of elements.
Let us consider the matrix test shown in Fig. 3, in terms of the steps of MEZW algorithm. Initialization step will be same as the EZW [2] algorithm, initializing the threshold by T0
9. a) Significance Test
The wavelet coefficients are scanned for the path presented in Fig. 2. Each coefficient is assigned a significance symbol (P, N, Z, T, P t and N t ), by comparing each coefficient with the actual thres hold ( )
j o j T T 2 =, where j is the iteration count):
? If a coefficient is greater than the threshold then it is called significant. If a coefficient is tested and found to be significant, its descendants must also be tested. If at least one descendant is significant the it
10. Global Journal of C omp uter S cience and T echnology
Volume XV Issue II Version I
11. Year ( )
H is encoded as P or N symbol. If the sign of the significant coefficient is positive, then this coefficient will be coded as P.
? This is the case for the coefficients {63, 49 and 47} in the matrix test (Fig. 4).
? If the coefficient is greater than the threshold and its sign is negative then this is coded as N. This is the case for the coefficient {?34} in the matrix test (Fig. 4).
? If a coefficient is less than its threshold value, then it will be considered as insignificant coefficient. If a coefficient is insignificant, then its descendent must be tested. If all of its descendants are insignificant, then it is encoded as a Pt or Nt symbols. If the symbol is positive, then the coefficient is coded as Pt symbol. This is the case for the coefficient {49} in the matrix test (Fig. 4).
? If the symbol is positive, then the coefficient is not coded as a symbol.
? If a wavelet coefficient is insignificant and all of its descendants are also insignificant, then it is coded as a zero tree T symbol. Like coefficient {23} in the matrix test (Fig. 4)
? The coefficient is insignificant but has some significant descendants then it is coded isolated zero Z symbol. This is the case for the coefficients {-31 and 14} (Fig. 4). By applying the MEZW to the matrix in Fig. 4 IV.
12. Proposed Method
As we know, after the wavelet transform of the image [1], the energy is concentrated in the low frequency part of the image. Most of the information is present in the low frequency part only. The traditional Embedded Zerotree Wavelet [2] coding approach, code all the frequency band of wavelet coefficients as the same importance without considering the amount of information in each frequency band. There is no difference if the sub band is a low frequency band or a high frequency band. Our proposed technique overcomes this limitation of EZW algorithm. This method divides the image into some sub-blocks. The sub image with low frequency, containing higher amount of information is compressed lossless by DPCM method. Lossless compression of the lower frequency sub band will increase the Peak Signal to Noise Ratio (PSNR). The modified EZW (MEZW) [3] coding and Run Length Encoding (RLE) [6] methods are used to compress the sub-images with high frequency (fig. 5). The high frequency content is less important, compressed using lossy method MEZW. The Modified EZW algorithm generates less Zero tree root symbol (Z) in comparing to EZW. RLE [6] coding for the use of this kind of relevance precisely.
13. Simulation Results
Lena image [2] is used as the test image. The Lena image of resolution 256 * 256. The bit depth of the image is 8 bits per pixel. First of all, using Haar wavelet for lifting decomposition of the image and then using the proposed method of compression. The quality of reconstruction image is calculated in terms of a parameter called peak signal to noise ratio (PSNR). PSNR (dB) performance and compression ratio (CR) performance is calculated using the following formulae.
? ? ? ? ? ? = MSE dB PSNR 255 log 10 ) ( 2 10Here, the mean square is:
( ) 2 1 1 1 ? ? = = ? × = n i m j j i y x m n MSEWhere n, m is the image size, xi the initial image and yj the reconstructed image.
m n bits coded of number bpp CR × = _ _ _ ) (Compression results of the proposed approach are compared with the MEZW [3] approach and DPCM [5] algorithm. The results obtained by proposing algorithm indicate that the use of sub band decomposition and different compression methods for different sub band of the image results in a significant increase in the signal to noise ratio of the image. The proposed algorithm is compared with MEZW [3] algorithm (fig. 6). With each iteration or scan pass the PSNR is increasing. For each scan pass proposed algorithm results in an approximate 20 dB large PSNR in comparing to MEZW [3]. Comparison of PSNR of different sub bands and MEZW [3] algorithm is presented in fig. 8. When comparing to DPCM [5] algorithm (fig. 7), there also increases in the PSNR value, but is less in comparison to previous comparison.
Compression ratio is large for the proposed technique. After each pass, value of compression ratio increase, so as the PSNR.
14. VI.
15. Conclusion
As the amount of information content is different for each frequency sub band of the image, in this paper, we proposed an image compression algorithm based on the high and low frequency distribution of wavelet coefficients. The results are compared to conventional DPCM and MEZW [3] approach for PSNR, resulting in improved PSNR. So we conclude that we use a different compression technique for each sub band, according to the amount of valuable information in the particular band. This will allow us to use the lossless technique for a crucial part of the image, results in an increased PSNR. We also find an approximated range, between twelve to fourteen, there is a negligible change in the PSNR of different sub bands.

| An Enhanced Wavelet based Image Compression Technique | ||||||||||||
| 63 | -30 | 9 | 10 | 0 | 0 | 0 | 0 | 7 | - | 12 | 7 | |
| 13 | ||||||||||||
| -31 | 23 | -14 | 13 | 0 | 0 | 0 | 0 | 3 | 4 | 6 | 1 | |
| 0 | 0 | 0 | 0 | 5 | -7 | 3 | 9 | |||||
| 15 | 14 | 3 | -12 | |||||||||
| 0 | 0 | 0 | 0 | 4 | -2 | 3 | 9 | |||||
| -9 | -7 | -14 | 8 | |||||||||
| -5 | 9 | -1 | 7 | 4 | -6 | -2 | 2 | |||||
| 3 | 0 | -3 | 2 | 2 | -2 | 0 | 4 | |||||
| 2 | -3 | 6 | 4 | 3 | 6 | 3 | 6 | |||||
| 5 | 11 | 5 | 6 | 0 | 3 | -4 | 4 | |||||
| Year | ||||||||||||
| DPCM Encoding | Scan | MEZW MEZW + Run Length Encoding | Proposed Algorithm | Volume XV Issue II Version I | ||||||||
| Times | Algorithm PSNR(dB) | PSNR(dB) | ( ) | |||||||||
| 5 7 9 Scan Times 5 | LL 13.48 37.65 46.71 62.41 HL LH HH Average 40.06 13.48 42.83 53.84 70.38 45.13 13.48 44.83 61.90 77.72 49.48 Comparison of MEZW and Proposed 22.35 25.34 28.84 approach in terms of PSNR Table II. DPCM Algorithm Proposed Algorithm PSNR(dB) PSNR(dB) LL HL LH HH Average 18.61 14.63 19.92 24.49 28.48 21.88 | Global Journal of C omp uter S cience and T echnology | ||||||||||
| 7 | 18.61 | 17.83 19.92 24.49 28.48 22.68 | ||||||||||
| 9 | 18.61 | 22.00 19.92 24.49 28.48 23.72 | ||||||||||
| Comparison of DPCM and Proposed | ||||||||||||
| approach in terms of PSNR | ||||||||||||
| Year |
| ( ) |